Merge sort algorithm

Fundamental

The merge sort algorithm uses the idea of divide and conquer, which reduces the big things to small ones and solves the small thing recursively, then gather the solutions together! The idea of divide and conquer includes the divide, resolve, and merge processes. Now let’s break down the merge sort algorithm into these three processes and see how each step is implemented:

1. Divide: divide the sequence to be sorted into two subsequences (usually from the middle).
2. Resolve: call the resolve function recursively on subsequences until the subsequence can be sorted directly.
3. Merge: merge the sorted subsequences to get the sorting solution of the parent sequence.

Implementation

The following code is the Python version implementation with animated visualization:

Firstly, let’s look at the logic of divide and resolve parts, which correspond to the solve function in the code: the solve function is responsible for sorting the interval($[l, r)$) in the given sequence. When there is more than one element in the interval($l < r-1$), The algorithm divides the interval into left and right parts($[l, m)$, $[m, r)$), and calls the solve function recursively until the sub-problem is resolved.

Secondly, let’s take a look at the merge function: the merge function merges two consecutive ordered sequences into one ordered sequence. The algorithm needs to take the smaller element from the head of the two subsequences at a time and place them in a temporary array(merge_list) in ascending order. After all the elements in the two subsequences are taken out, copy merge_list to the original sequence.

import algviz

class MergeSort():
    def __init__(self, nums_):
        self.viz = algviz.Visualizer(2.0)
        self.nums = self.viz.createVector(nums_, name='Numbers', cell_size=(40, 200), histogram=True)
        self.merge_list = self.viz.createVector(name='Merge list', show_index=False)
        self.tree = algviz.RecursiveTree(self.viz)
        self.solve(0, len(nums_))
    
    def solve(self, l, r):
        if l < r - 1:
            self.tree.forward('{}:{}'.format(l, r))
            m = (l + r)//2
            self.solve(l, m)
            self.solve(m, r)
            self.nums.mark(algviz.color_gray, 0, l, hold=True)
            if r < len(self.nums):
                self.nums.mark(algviz.color_gray, r, len(self.nums), hold=True)
            self.merge(l, m, r)
            self.tree.backward()
            self.nums.removeMark(algviz.color_gray)
    
    def merge(self, l, m, r):
        # Take out the smaller elements in the subsequence in turn and place them in the merge_list.
        ll = l; mm = m
        self.viz.display()
        while ll < m and mm < r:
            if self.nums[ll] > self.nums[mm]:
                self.merge_list.append(self.nums[mm])
                self.nums.mark(algviz.color_gold, mm); self.nums.mark(algviz.color_dark_green, ll)
                self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
                mm += 1; self.viz.display(1)
            else:
                self.merge_list.append(self.nums[ll])
                self.nums.mark(algviz.color_gold, ll); self.nums.mark(algviz.color_dark_green, mm)
                self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
                ll += 1; self.viz.display(1)
        while ll < m:
            self.merge_list.append(self.nums[ll])
            self.nums.mark(algviz.color_gold, ll)
            self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
            ll += 1; self.viz.display(1)
        while mm < r:
            self.merge_list.append(self.nums[mm])
            self.nums.mark(algviz.color_gold, mm)
            self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
            mm += 1; self.viz.display(1)
        # Copies the merge_list into the origin subsequence to be resolved.
        self.viz.display()
        for i in range(l, r):
            self.merge_list.mark(algviz.color_spring_green, 0)
            self.nums[i] = self.merge_list.pop(0)
            self.nums.mark(algviz.color_spring_green, i)
            self.viz.display()

solver = MergeSort([5, 3, -2, 3, -1, 1, 4])

You can run this code snippet directly after installing algviz locally! For environment configuration, please refer to the Installation page.

Animation Demo

The animation can be divided into three parts: RecursiveTree, Numbers, and MergeList.

• The RecursiveTree shows the current recursive state of the algorithm, each sub-problem corresponds to a node in the tree. Newly generated sub-problem are marked in green, resolved sub-problem are marked in grey, and sub-problem currently being worked on are marked in red.
• Ranges in Numbers that are not currently being processed are marked in gray, while elements currently being compared are marked in green (larger values) and orange (smaller values).

Features

Merge sort is a comparison-based sorting algorithm, which is not only relatively stable but also very efficient in time. But this algorithm consumes more space, so usually, we use merge sort if we have extra space, and use quicksort if we just want to modify the given sequence.

Time Complexity

Some readers may find that the algviz.RecursiveTree class is used in the above code implementation. The RecursiveTree can help us observe the recursive process of the algorithm. You can refer to the Introduction to the RecursiveTree tool page for more information about the RecursiveTree.

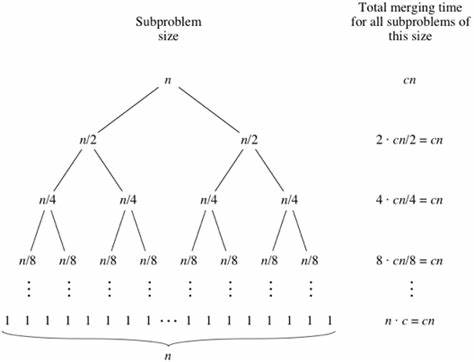
Looking at the figure below, it can be found that the maximum depth of the recursive tree is $O(log_2^n)$, and the merge step of each layer requires $O(n)$ basic operations. So, the overall time complexity of the algorithm is $O(n \cdot log_2^n)$.

Space Complexity

The stack depth of the recursive process is $O(log_2^n)$, and $O(n)$ space is required for the merge operations to handle copy merge_list. So, the space complexity of the merge sort algorithm is $O(log_2^n) + O(n)$, which is equivalent to $O(n)$.