基本原理
归并排序算法使用了分治的思想(Divide and Conquer),既大事化小、小事化了,先散后聚! 分治思想包含了分割、解决和合并三个过程,下面我们将归并排序算法分解为这三个过程,看一下每一步是如何实现的:
- 分割: 将要排序的序列分割成两段(一般是从中间分割),分割后可以得到两个子序列。
- 解决: 对子序列递归的调用归并排序算法,直到子序列可以被直接排序(只剩一个元素)。
- 合并: 将排好序的子序列进行合并,从而得到有序的父序列。
算法实现
下面的代码是带动画可视化的 Python 版本实现:
首先看分割和解决部分的逻辑,对应代码中的 solve 函数: solve 函数负责对给定数组中的 $[l, r)$ 区间进行排序(这里设计成左闭右开区间是为了方便做边界检测),当区间中有一个以上元素时(即 $l < r-1$),算法将区间分成左右两部分($[l, m)$, $[m, r)$),并对左右两部分分别递归的调用 solve 函数进行求解。
然后看一下合并部分的逻辑,对应代码中的 merge 函数:merge 函数将两个紧挨着的有序序列合并成一个整体有序的序列。算法需要每次从两个子序列的头部取出较小的元素,先将它们按照从小到大的顺序放到一个临时数组中(merge_list),等两个子序列中的元素被全部取出后,再将 merge_list 复制到原始序列中去即可。
import algviz
class MergeSort():
'''
nums_:list() 要排序的数组。
'''
def __init__(self, nums_):
self.viz = algviz.Visualizer(2.0)
self.nums = self.viz.createVector(nums_, name='Numbers', cell_size=(40, 200), histogram=True)
self.merge_list = self.viz.createVector(name='Merge list', show_index=False)
self.tree = algviz.RecursiveTree(self.viz)
self.solve(0, len(nums_))
'''
l,r:int 排序数组的左右边界(左闭右开)。
'''
def solve(self, l, r):
if l < r - 1:
self.tree.forward('{}:{}'.format(l, r))
m = (l + r)//2
self.solve(l, m)
self.solve(m, r)
self.nums.mark(algviz.color_gray, 0, l, hold=True)
if r < len(self.nums):
self.nums.mark(algviz.color_gray, r, len(self.nums), hold=True)
self.merge(l, m, r)
self.tree.backward()
self.nums.removeMark(algviz.color_gray)
'''
l,m,r:int 合并序列的左边界、中间分割点和右边界。
'''
def merge(self, l, m, r):
# 依次取出子序列中较小的元素放置到缓存数组中。
ll = l; mm = m
self.viz.display()
while ll < m and mm < r:
if self.nums[ll] > self.nums[mm]:
self.merge_list.append(self.nums[mm])
self.nums.mark(algviz.color_gold, mm); self.nums.mark(algviz.color_dark_green, ll)
self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
mm += 1; self.viz.display(1)
else:
self.merge_list.append(self.nums[ll])
self.nums.mark(algviz.color_gold, ll); self.nums.mark(algviz.color_dark_green, mm)
self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
ll += 1; self.viz.display(1)
while ll < m:
self.merge_list.append(self.nums[ll])
self.nums.mark(algviz.color_gold, ll)
self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
ll += 1; self.viz.display(1)
while mm < r:
self.merge_list.append(self.nums[mm])
self.nums.mark(algviz.color_gold, mm)
self.merge_list.mark(algviz.color_gold, len(self.merge_list)-1); self.viz.display()
mm += 1; self.viz.display(1)
# 将排好序的数组复制到元素序列中。
self.viz.display()
for i in range(l, r):
self.merge_list.mark(algviz.color_spring_green, 0)
self.nums[i] = self.merge_list.pop(0)
self.nums.mark(algviz.color_spring_green, i)
self.viz.display()
solver = MergeSort([5, 3, -2, 3, -1, 1, 4])
您可以在本地安装 algviz 后直接运行该代码片段!环境配置请参考:安装步骤
动画演示
动画包括三个数据结构:递归树(Recursive tree)、排序数组(Numbers)和临时数组(Merge list)。
- 递归树用于展现算法当前的递归状态,每个子问题对应树中的一个节点(对应区间 $[l, r)$)。新产生的子问题使用绿色标记,已解决的子问题使用灰色标记,而当前正在处理的子问题使用红色标记。
- 排序数组中当前未被处理的区间使用灰色标记,而当前正在进行比较的元素使用绿色(较大值)和橙色(较小值)标记。
算法特点
归并排序属于基于比较的排序算法,它不仅比较稳定,在时间上也是非常高效的,但是这种算法比较消耗空间,所以通常我们在外部排序中使用归并排序,而在内部排序中使用快速排序取代之。
时间复杂度
细心的读者可能会发现,上述代码实现中有使用到了递归树( algviz.RecursiveTree )这个类,它可以帮助我们观察算法的递归过程,有兴趣的读者可以阅读递归算法分析工具 RecursiveTree 使用介绍。
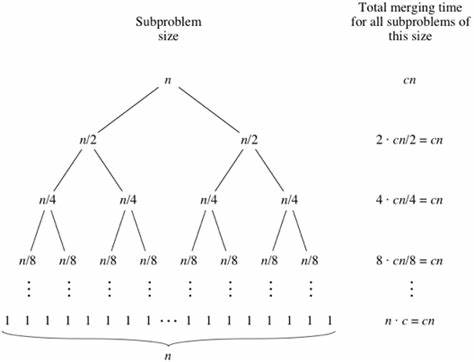
观察下图可以发现,递归树的最大深度为 $O(log_2^n)$,而每一层的 merge 步骤需要 $O(n)$ 次的基本操作,因此算法的整体时间复杂度为两者的乘积 $O(n \cdot log_2^n)$。
空间复杂度
递归过程的压栈深度为 $O(log_2^n)$,同时合并(merge)操作需要 $O(n)$ 的辅助空间(merge_list)来处理临时的排序结果,因此归并排序算法的空间复杂度为 $O(log_2^n) + O(n)$,等价于 $O(n)$。
本文遵守 Attribution-NoDerivs 2.0 Generic许可协议。 

